프로그래밍의 도를 찾아서

Fermat 점(페르마 점)의 위치와 그 성질에 대한 두 가지 증명

목차

해석적인 증명

본 증명은 Lagrange 승수법을 통해 조건부 극값 문제를 해결하여 주어진 명제를 증명한다. 가장 단순하면서도 계산이 복잡한 방식이다.

삼각형 ABC\mathrm{ABC}와 그 내부의 점 K\mathrm K를 잡자. 이 때,

AB=c,BC=a,CA=b,AP=x,BP=y,CP=z,∠APB=γ=2π−α−β,∠BPC=α,∠CPA=β\mathrm{AB} = c, \mathrm{BC} = a, \mathrm{CA} = b,\\ \mathrm{AP} = x, \mathrm{BP} = y, \mathrm{CP} = z,\\ \angle \mathrm{APB} = \gamma = 2\pi - \alpha - \beta, \angle \mathrm{BPC} = \alpha, \angle \mathrm{CPA} = \beta

으로 설정하고, 함수 f:E→Rf: \mathbb{E} \rightarrow \mathbb{R}는 f(P)=x+y+zf(P) = x + y + z로 정의하자. Fermat 점을 찾는 문제가 ff의 극값을 구하는 문제로 바뀌었다. 단, 주어진 세 점 A,B,C\mathrm{A, B, C}는 삼각형을 이루므로 다음의 세 조건을 만족한다.

x2+y2−2xycos⁡(2π−α−β)=c2,y2+z2−2yzcos⁡α=a2,z2+x2−2zxcos⁡β=b2x^2 + y^2 - 2xy \cos (2\pi - \alpha - \beta) = c^2,\\ y^2 + z^2 - 2yz \cos \alpha = a^2,\\ z^2 + x^2 - 2zx \cos \beta = b^2

이제 다음과 같이 E\mathbb E에서 R\mathbb R로 가는 세 함수를 정의할 수 있다:

g1(P)=x2+y2−2xycos⁡(α+β)−c2,g2(P)=y2+z2−2yzcos⁡α−a2,g3(P)=z2+x2−2zxcos⁡β−b2g_1 (P) = x^2 + y^2 - 2xy \cos (\alpha + \beta) - c^2,\\ g_2 (P) = y^2 + z^2 - 2yz \cos \alpha - a^2,\\ g_3 (P) = z^2 + x^2 - 2zx \cos \beta - b^2

Lagrange 승수법을 사용하기 위해 다음과 같은 새로운 함수 f~:E→R\tilde f: \mathbb{E} \rightarrow \mathbb{R}를 정의하자:

f~(P)=f(P)−∑i=13λigi(P)\tilde f(P) = f(P) - \sum_{i = 1}^3 \lambda_i g_i (P)

이제 좀 골치 아픈 작업이 남았다—f~\tilde f의 극값을 구하기 위해 x,y,z,α,βx, y, z, \alpha, \beta에 대해서 식을 편미분하자.

(1) ∂f~∂x=1−2λ1x+2λ1ycos⁡(α+β)−2λ3x+2λ3zcos⁡β=0(2) ∂f~∂y=1−2λ1y+2λ1xcos⁡(α+β)−2λ2y+2λ2zcos⁡α=0(3) ∂f~∂z=1−2λ2z+2λ2ycos⁡α−2λ3z+2λ3xcos⁡β=0(4) ∂f~∂α=2λ1xysin⁡(α+β)+2λ2yzsin⁡α=0(5) ∂f~∂β=2λ1xysin⁡(α+β)+2λ3zxsin⁡β=0(1)\ \frac{\partial \tilde f}{\partial x} = 1 - 2 \lambda_1 x + 2 \lambda_1 y \cos (\alpha + \beta) - 2 \lambda_3 x + 2 \lambda_3 z \cos \beta = 0\\ (2)\ \frac{\partial \tilde f}{\partial y} = 1 - 2 \lambda_1 y + 2 \lambda_1 x \cos (\alpha + \beta) - 2 \lambda_2 y + 2 \lambda_2 z \cos \alpha = 0\\ (3)\ \frac{\partial \tilde f}{\partial z} = 1 - 2 \lambda_2 z + 2 \lambda_2 y \cos \alpha - 2 \lambda_3 z + 2 \lambda_3 x \cos \beta = 0\\ (4)\ \frac{\partial \tilde f}{\partial \alpha} = 2 \lambda_1 xy \sin (\alpha + \beta) + 2 \lambda_2 yz \sin \alpha = 0\\ (5)\ \frac{\partial \tilde f}{\partial \beta} = 2 \lambda_1 xy \sin (\alpha + \beta) + 2 \lambda_3 zx \sin \beta = 0

항 하나가 완전히 일치하는 (4)와 (5)를 연립하면 λ2sin⁡αλ3sin⁡β=xy\frac{\lambda_2 \sin \alpha}{\lambda_3 \sin \beta} = \frac x y이 된다. 이 때 x=kλ2sin⁡αx = k \lambda_2 \sin \alpha라고 두고 다시 (4)나 (5)에 대입하면, x,y,zx, y, z 모두 k,α,βk, \alpha, \beta만으로 표현할 수 있게 된다.

x=kλ2sin⁡α,y=kλ3sin⁡β,z=kλ1sin⁡(αβ)x = k \lambda_2 \sin \alpha,\\ y = k \lambda_3 \sin \beta,\\ z = k \lambda_1 \sin (\alpha _ \beta)

이렇게 다시 쓴 x,y,zx, y, z를 (1)–(3)에 대입하여 식을 정리하고 sin⁡(α+β)=sin⁡αcos⁡β+cos⁡αsin⁡β\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta를 대입하면,

sin⁡α=X,sin⁡β=X,sin⁡(α+β)=X\sin \alpha = X,\\ \sin \beta = X,\\ \sin (\alpha + \beta) = X

가 나온다. 이 때, XX는 식을 정리하면서 나온 어떤 값이다. 결국 α=β=120∘\alpha = \beta = 120^\circ를 알 수 있다.

그런데, 이 증명에는 흠이 있는데, Lagrange 승수법의 한계상, 이미 ff는 극값을 가진다는 것이 전제된다. 즉, 필요 조건일 뿐이지 충분 조건이 되지 않는다. 예컨데 삼각형의 한 내각이 120돌르 넘는다면, Fermat 점에서 각 꼭짓점들을 이은 직선들은 서로 이루는 각이 120도가 될 수 없다.

이에 우리는 이 문제를 해결할 수 있는 기하적인 증명을 제시한다.

기하적인 증명

삼각형 ABC\mathrm{ABC}와 그 내부의 한 점 F′F'를 잡자.

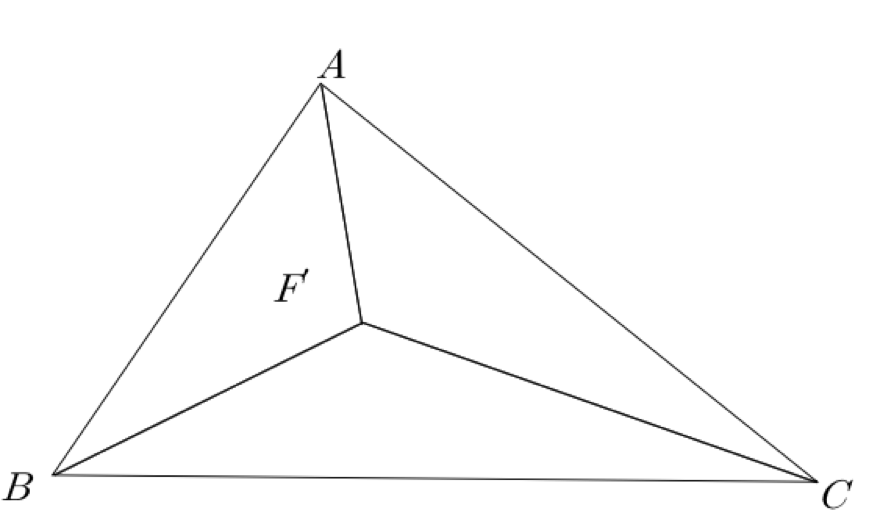
Figure 1

이 △ABC\triangle \mathrm{ABC}를 점 B\mathrm B에 대해 반시계 방향으로 60도 회전한다. 이렇게 회전된 삼각형과 점을 각각 △A′BC,F′′\triangle \mathrm{A'BC}, F''으로 두자.

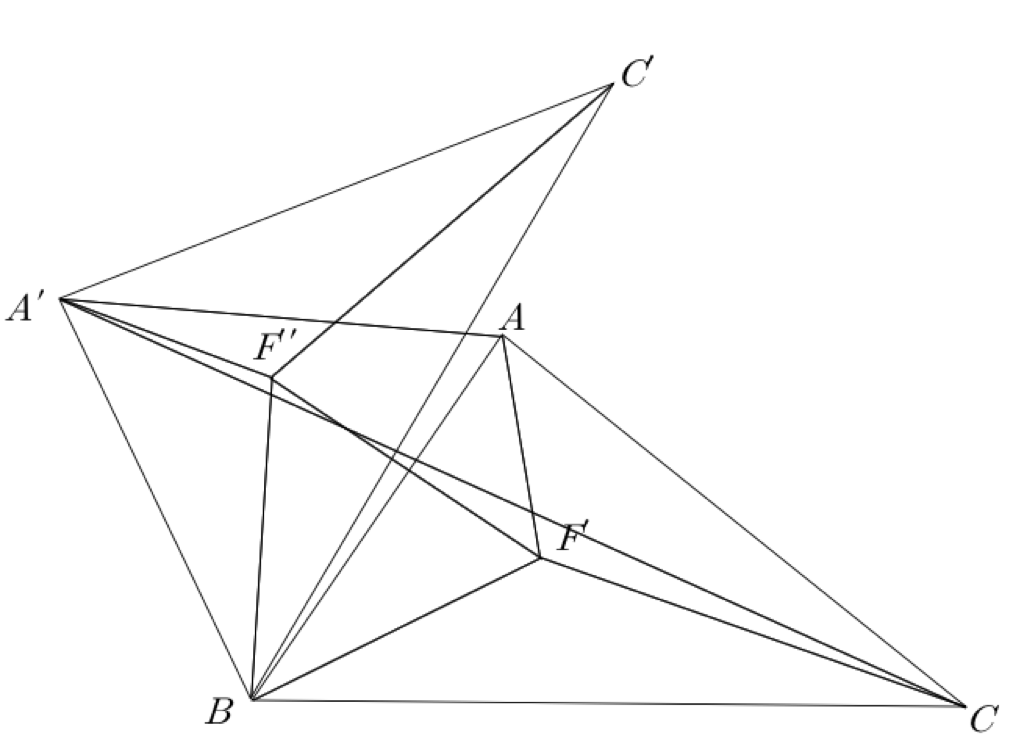
Figure 2

그렇다면 AF′+BF′+CF′=A′F′′+F′′F′+F′C\mathrm{AF' + BF' + CF' = A'F'' + F''F' + F'C}이며, 이의 최솟값은 A′C\mathrm{A'C}가 된다. (Euclid 평면에서 최단거리는 직선이기 때문이다.) A′B=BA=AA′\mathrm{A'B = BA = AA'}이므로 △AA′B\triangle \mathrm{AA'B}는 정삼각형이다. 즉, A′\mathrm A'은 △ABC\triangle \mathrm{ABC} 외부에 AB\mathrm{AB}와 정삼각형을 이루도록 잡은 점이다.

Figure 3

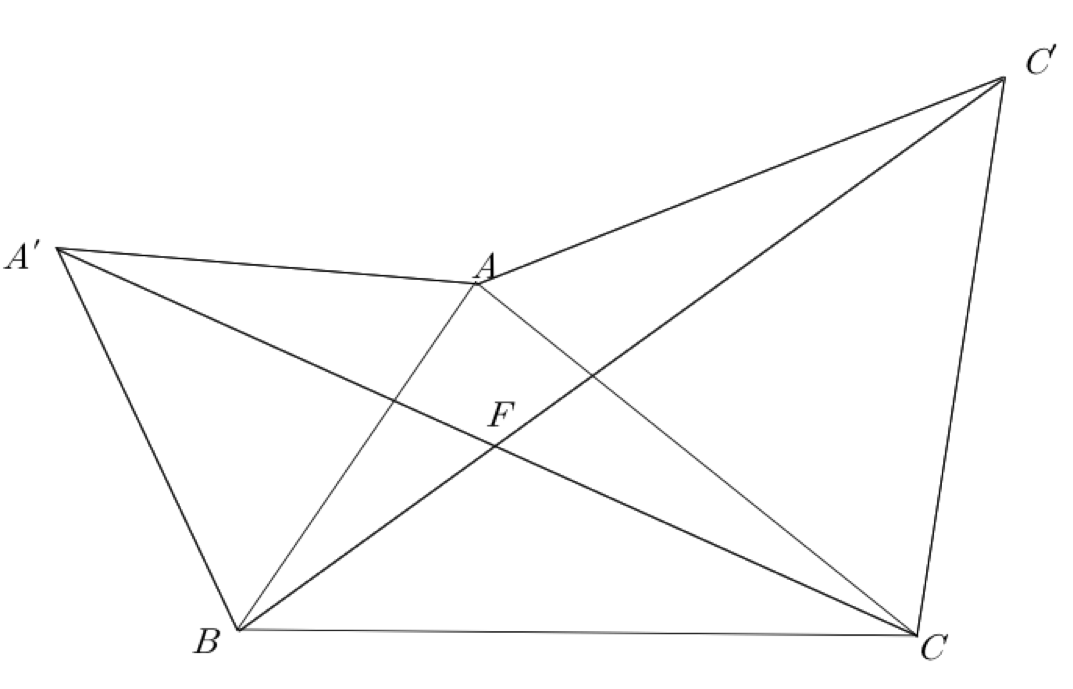
마찬가지로, △BB′C\triangle \mathrm{BB'C}가 정삼각형이 되도록 B′\mathrm B'을 △ABC\triangle \mathrm{ABC} 밖에 잡을 수 있다. 따라서 AF′+BF′+CF′\mathrm{AF' + BF' + CF'}이 최소인 F′\mathrm F'은 CA′\mathrm{CA'}과 AB′\mathrm{AB'}의 교점에 위치할 때이며, 이를 F\mathrm F라고 하자.

또한, A′A=BA,∠A′AC=∠BAC′,AC=AC′\mathrm{A'A = BA, \angle A'AC = \angle BAC', AC = AC'}이므로 △A′AC≡△BAC (SAS)\triangle \mathrm{A'AC} \equiv \triangle \mathrm{BAC}\ (SAS)이다. 결국 ∠ABF=∠AA′F\angle \mathrm{ABF} = \angle \mathrm{AA'F}이어서 A,A′,B,F\mathrm{A, A', B, F}는 concyclic, 즉 한 원 위에 있다. 따라서 ∠AFB=180∘−∠AA′B=120∘\mathrm{\angle AFB = 180^\circ - \angle AA'B = 120^\circ}이다.

그런데, 위 증명에서는 삼각형의 내각이 모두 120도 이하일 경우만을 고려한 것이다. 왜인지 알겠는가? A,A′,B,F\mathrm{A, A', B, F}가 한 원 위에 있다고 하였을 때, ∠BAC\angle \mathrm{BAC}가 120도를 넘었더라면 네 점의 외접원 내부에 A\mathrm A가 들어와 문제가 되기 때문이다. 이런 경우를 따로 고려해줘야한다.

간단히 개요만 설명한다. ∠BAC\angle \mathrm{BAC}가 120도를 넘는다고 하자. 그렇다면 삼각형 내부의 어떤 점이든 각 꼭짓점까지의 거리 합이 AB+AC\mathrm{AB + AC}보다 작은 점이 없다는 것은 위 증명을 조금 변형하여 알 수 있다. 이제 아래와 같은 lemma를 설정하자.

삼각형 외부의 어떤 점이든, 각 꼭짓점까지의 거리 합은 그 삼각형 둘레에 존재하는 점에서 각 꼭짓점까지의 거리의 합보다 작다.

삼각형의 각 변을 직선으로 연장하여 평면을 총 6구역으로 나눌 수 있는데, 각 구역에 존재하는 점에서 각 꼭짓점까지의 거리 합보다 작은 삼각형 둘레 상의 점을 쉽게 찾을 수 있다. 일반성을 잃지 않고 삼각형의 꼭짓점이 그 무한 영역의 끝이 아닌 경우와 삼각형의 변이 무한 영역의 경계인 경우 두 구역에 대해서만 확인해보면 된다. 이렇게 lemma를 증명하면, A\mathrm A가 Fermat 점이 됨을 알 수 있다.