목차
도입
프랙탈(fractal) 또는 프랙털은 일부 작은 조각이 전체와 비슷한 기하학적 형태를 말한다. 이런 특징을 자기 유사성이라고 하며, 다시 말해 자기 유사성을 갖는 기하학적 구조를 프랙탈 구조라고 한다. -- 한글 위키백과
프랙탈 자체에 관하여는 위키백과가 훌륭히 서술을 하고 있으니, 여기서는 자세히 설명하지 않겠다. 코딩의 관점에서 프랙탈은 기하적으로 재귀적(recursive)인 형태를 만드는 것이기 때문에, 반복문이나 재귀 호출을 연습할 때 흔히 쓰이는 예제이다. (흔히 별찍기 문제라고 불리우는 것들 중 어려운 축에 속하는 문제들)
본 글에서는 Mandelbrot 집합 같은 프랙탈이 아닌, 단순한 Sierpinski 삼각형이나
카펫의 형태를 다룬다.
먼저 명령형(imperative) 방식과 선언형(declarative) 방식을 비교한 후,
재귀(recursion)에 대해 간단히 소개한다.
이후 SwiftUI의 재귀적 View 구성으로 Sierpinski 카펫과 삼각형을 구성해본다.
그러나 이 방식은 성능면에서 한계가 있는데,
Shape를 사용한
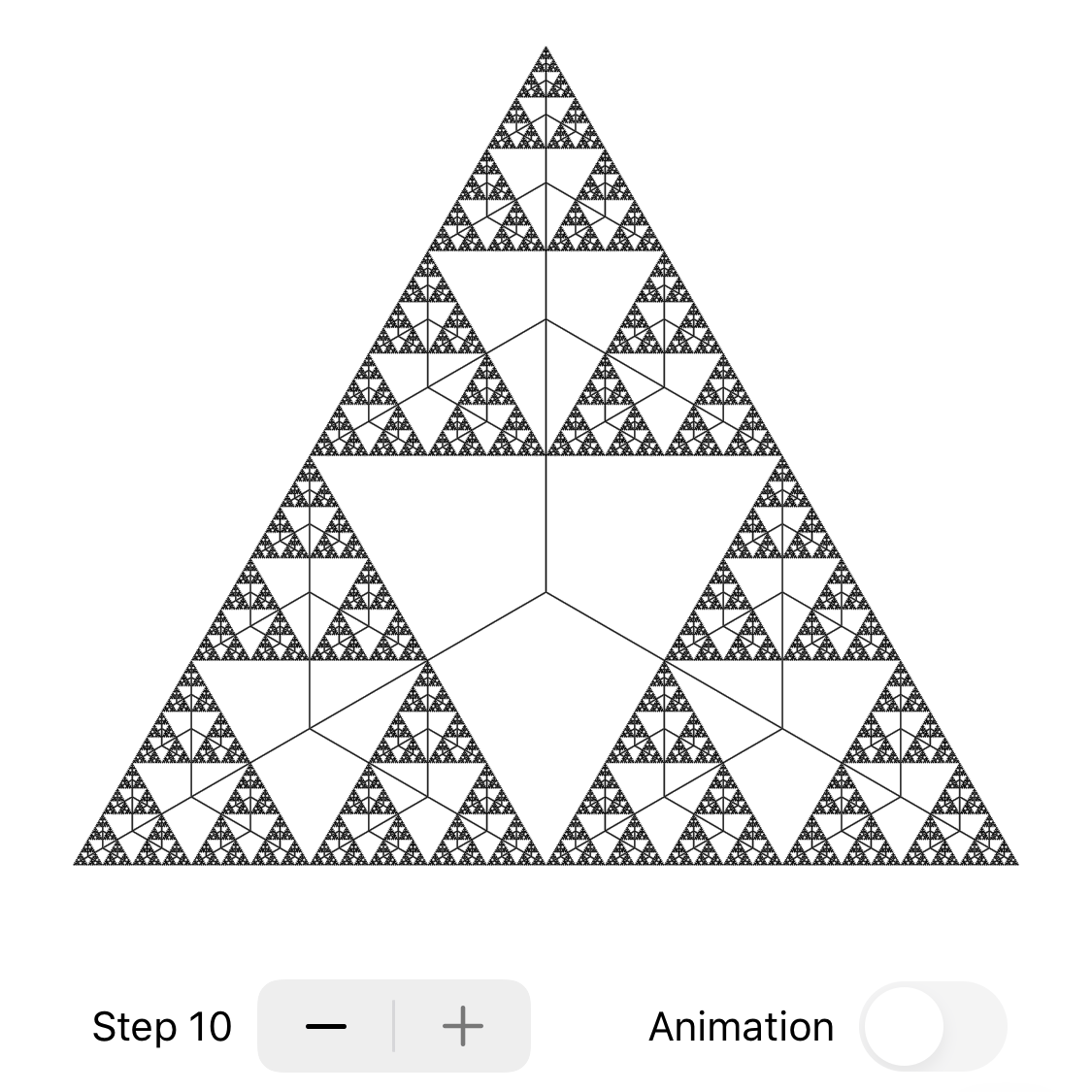
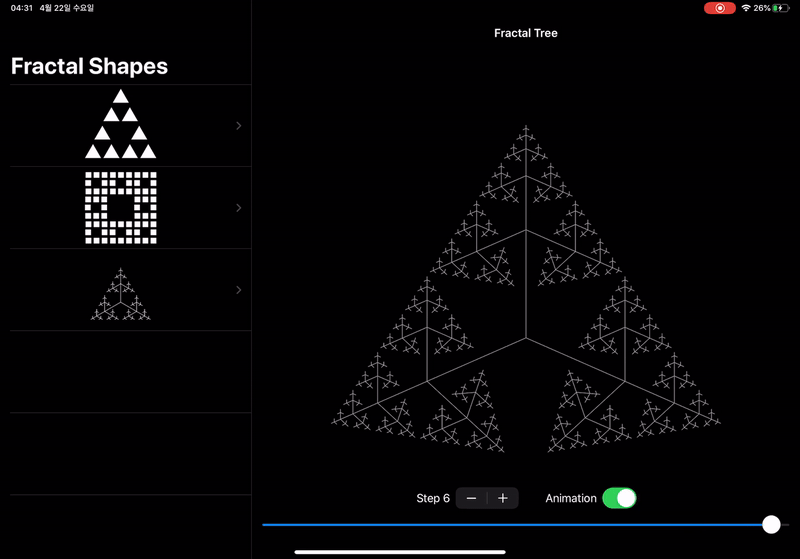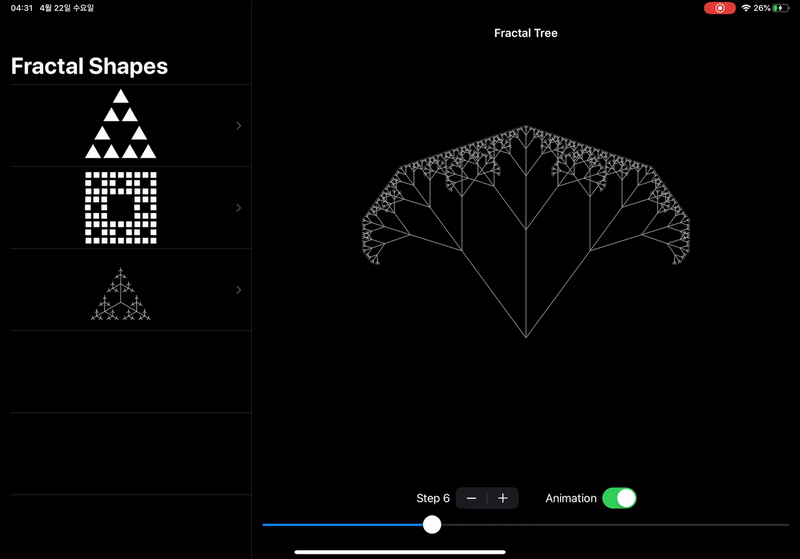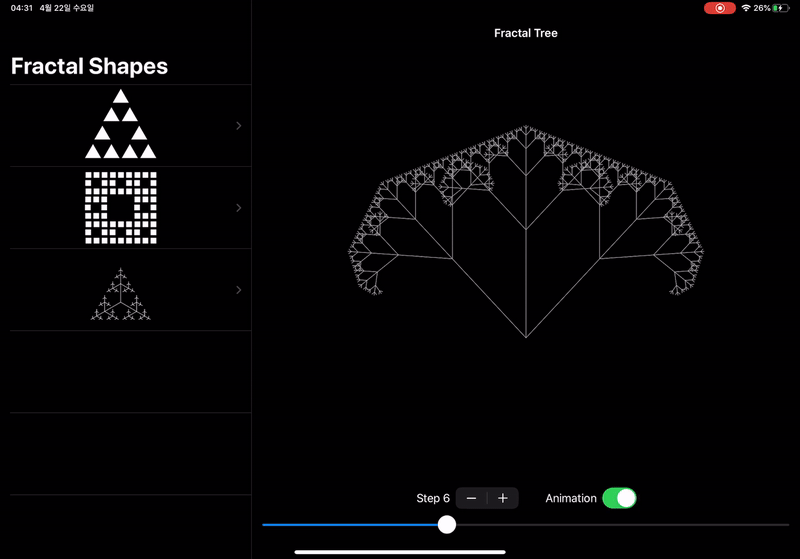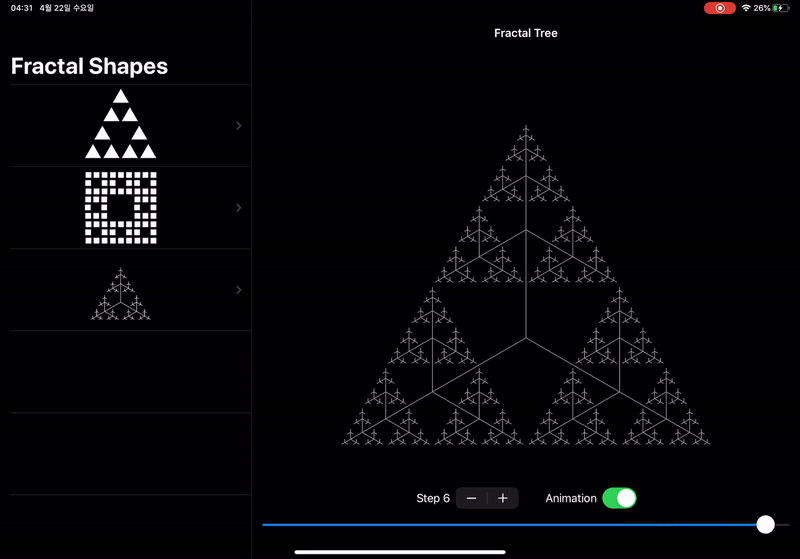
다른 방식으로 접근하여 fractal tree (본 글의 맨 위 스크린 샷)를 구현해본다.
나아가, SwiftUI의
Animatable 을
활용하여 fractal tree의 애니메이션을 구현한다.
완성된 결과는 아래 GIF와 같으며, 전체 결과물은
GitHub에서 확인할 수 있다.
명령형과 선언형
진행하기에 앞서, 본 글에서는 명령형과 절차적 프로그래밍을 같은 의미로 혼용하여
사용할 것이라는 것을 알린다.
(후자는 함수나 for 문과 같은 control flow를 사용한다는 의미를 포함하기에
약간의 차이가 있지만, 본 글의 맥락에서는 큰 문제가 되지 않는다.)
절차적으로 프랙탈 '별찍기'
아래 코드는 Sierpinski 삼각형 형태의 '별찍기' 코드이다.
def sierpinski(step: int):
if step == 1:
return [" * ", " * * ", "*****"]
previous = sierpinski(step - 1)
result = []
mid = len(previous[0]) // 2 + 1
for i in range(mid):
result.append(" " * mid + previous[i] + " " * mid)
for i in range(mid, 2 * mid):
result.append(previous[i % mid] + " " + previous[i % mid])
return result
m = int(input())
for line in sierpinski(m):
print(line)Python을 모르더라도 Swift를 안다면 읽는데 무리가 없을 간단한 코드이다. (SwiftUI 글에 왜 Python 코드냐면, 이미 필자가 Python 2로 예전에 짜둔 것이 있어서 그냥 Python 3로 옮겨왔다.) 위 코드에 4를 입력으로 주면 아래와 같이 출력된다:

뭐 상당히 싱거운 결과긴 하지만, 위 코드에서 강조하고 싶은 것은 그
절차적인 방식이다.
위 코드는 for 문을 사용해 Sierpinski 삼각형의 구조를 쪼갠 후, list에 더하는
것을 반복한다.
그런데 다시 생각해보면, 우리는 어떤 구조 안에 그 구조가 다시 반복되는 형태를
만들고 싶었던 것 뿐이다.
Sierpinski 삼각형은 그 구조가 세 꼭짓점 쪽에 무한히 반복되는 것이고 말이다.
만약 우리의 언어가 MS사의 PowerPoint였다면, 다음 영상에서처럼 간단히 삼각형의 위치를 드래그해 정해주는 것만으로도 Sierpinski 삼각형을 구현할 수 있었을 것이다:
(여담이지만, PowerPoint는 Turing 완전하다!)
Python 예시와 PowerPoint 예시의 차이점은, 후자는 선언적인(declarative) 성격을 가지는 반면 전자는 절차를 직접 명령했다는 것이다.
for 문과 재귀 호출
본격적으로 SwiftUI에서 재귀적인 View를 구현하기 전에, 간단한 for 문과 재귀
호출을 비교해보도록 하자.
1부터 n까지를 출력하는 코드는 Swift에서 다음과 같이 작성할 수 있다:
for i in 1...n {
print(i)
}여기에 작성하기 민망할 정도로 간단한 코드이긴 하지만, OCaml과 같은 함수형
언어에서는 (물론 for문이 있기는 하지만 제한적이다) 보통 이런 간단한 작업을
포함한 모든 반복을 재귀 함수로 처리한다.
간단히 써보면,
let rec loop n =
if n < 1 then () else (
loop (n - 1);
print_int n;
print_newline ()
)와 같다.
재귀 호출에서 핵심은, 1부터 n까지 출력을 어떻게 하는지가 아니라 무엇을
하는지 강조하는 것이다.
1부터 n까지 출력하는 것은 1부터 n - 1까지 출력하기를 한 후, n을 출력하는
것이다.
이때 필요한 것은 종료 조건인데, 입력이 1보다 작은 값은 아무것도 하지 않으면
된다.
OCaml이라는 언어가 생소한 독자분들이 대다수겠지만, 위 코드에서는 이러한
재귀적인 사고 방식이 명확하게 드러날 것이다.
SwiftUI에서 재귀적 View 구성하기
다시 SwiftUI로 돌아와서, SwiftUI의 가장 큰 특징은 UIKit과 달리 선언적으로
layout을 정의할 수 있다는 점이다.
var body: some View { }안에 넣는 내용이 실제로 화면에 render되는 결과이다.
위의 for 문과 재귀 호출에 썼던 예시를 가져와서, SwiftUI에서 1부터 n을
'출력'하려면 어떻게 해야 할까?
SwiftUI의
ForEach를
사용하면 된다:
struct ContentView: View {
let n: Int
var body: some View {
VStack {
ForEach(0..<n) {
Text("\($0 + 1)")
}
}
}
}ContentView(n: 5)의 결과는 다음과 같다:
그런데 오늘 날씨가 안 좋거나해서 기분이 꼬였다면, 이를 재귀로 구현하고 싶은 마음이 들 수도 있다. 위에서 잠깐 보았던 OCaml 코드와 정확히 동일한 구조로 코드를 작성하면 된다!
struct ContentView: View {
let n: Int
var body: some View {
VStack {
if n < 1 {
EmptyView()
} else {
ContentView(n: n - 1)
Text("\(n)")
}
}
}
}다만 Swift(UI)에서는 OCaml과 다르게 if-then-else의 모든 가지를 갖출 필요가
없기 때문에, VStack안을 다음과 같이 간략화할 수 있다:
if n >= 1 {
ContentView(n: n - 1)
Text("\(n)")
}결과는 ForEach를 썼을 때와 완전히 동일하다.
Sierpinski 카펫과 삼각형
Sierpinski 카펫
먼저 Sierpinski 카펫을 구현해보자.
자기 자신의 형태를 첫 줄에 세 개, 둘째 줄에 양 끝에 두 개, 마지막 줄에 세 개를
넣는 방법이 가장 먼저 생각날 것이다.
다만 둘째 줄에 가운데 Spacer()을 통해 두 view를 분리한다면, 첫 줄과 마지막
줄에 포함된 view와 크기가 다르게 나온다.
따라서 둘째 줄에도 자기 자신을 세 개 넣는 대신, 가운데의 view는 보이지 않게
.hidden()을 사용하여 크기를 맞춘다.
다음과 같이 구현하면:
struct Carpet: View {
let n: Int
private var child: some View { Carpet(n: n - 1) }
private var defaultRow: some View {
HStack(spacing: 2) { child; child; child }
}
private var middleRow: some View {
HStack(spacing: 2) { child; child.hidden(); child }
}
var body: some View {
if n > 0 {
return VStack(spacing: 2) {
defaultRow; middleRow; defaultRow
}
.asAnyView()
} else {
return Rectangle()
.aspectRatio(1, contentMode: .fit)
.asAnyView()
}
}
}n = 0부터 5까지 아래와 같은 결과가 나온다.






이때 .asAnyView()는 AnyView로 감싸주는 extension이다:
extension View {
func asAnyView() -> AnyView {
AnyView(self)
}
}이는 Swift의
opaque 반환값을
요구하는 함수에서는 반환값이 모두 일치해야하기 때문에 AnyView로 타입을 지워준
것이다.
그렇지 않다면 위 코드의 if 문 안에서는 VStack으로 감싸진 some View,
else 문에서는 .aspectRatio(...)가 반환하는 또 다른 종류의 some View를
반환하여 문제가 된다.
다시 코드 내용으로 돌아가서, 위 코드의 종료 조건은 else 문의 Rectangle을
그리는 코드이다.
위 결과를 보면 알겠지만, 실제로 사각형을 그리는 부분은 재귀 호출에서 마지막
단계이고, 그 전 단계들은 모두 '배치'를 하는 과정이다.
실제로 Xcode에서 확인할 독자들이 계신다면, n = 4인 경우 그냥 Canvas에서는
render에 5초가 넘게 걸려 오류가 나기 때문에 Live Preview를 사용해서 확인을
하였다.
그리고
GitHub에 있는 버전은
위의 코드에서 변경점이 다소 있다.
해당 버전은 사각형의 크기에 비례하는 spacing을 주고, 각 사격형이 회전했을 때
서로 겹치지 않도록 Rectangle이 아니라 후술할 custom Shape을 사용하였다.
또한 n이 커졌을 때 사각형들의 끝이 일렬로 오지 않는 현상을 최대한 해결하기
위해 (위에서 사용하지 않았던) Spacer()과 GeometryReader의 조합을 사용하여
구현했다.
GeometryReader 등 layout에 관하여는
이 포스팅에서 자세히
확인할 수 있다.
Shape Protocol
SwiftUI에서는 삼각형을 기본적으로 제공하지 않는다.
이를 위해서는 Shape protocol을 따르는 struct를 만들어주면 된다.
Shape protocol을 따르기 위해서는
func path(in rect: CGRect) -> Path함수를 구현해주면 된다.
주어진 CGRect 안에서 자유롭게 그림을 그리면 된다!
이 _그림_의 type은 Path인데, 여기서는 세 method만 알면 된다:
public mutating func move(to p: CGPoint)
public mutating func addLine(to p: CGPoint)
public mutating func closeSubpath()굉장히 직관적인 이름을 가지는 함수들인데, 그래도 간단히 설명을 붙이자면
move(to:) 함수는 주어진 CGPoint로 Path를 그릴 '펜'을 옮기고,
addLine(to:) 함수는 현재 '펜'의 위치에서 주어진 CGPoint까지 선을 긋고,
closeSubpath는 현재의 부분 경로의 시작점까지 선을 그려서 닫는 것이다.
직접 사람이 펜을 가지고 그림을 그리는 것과 같은 방법이다.
정다각형 구현
path(in:) 함수를 구현하기 위해서는 먼저 그림을 그릴 도화지, 즉 CGRect의
범위 안에서 그려야 한다.
만약 여기를 벗어난다면 Shape의 frame을 벗어나는 획들이 나올
것이다(Shape도 View이다).
따라서 주어진 CGRect의 변 중 작은 것의 절반을 반지름으로 하는 내접원의
내접하는 정다각형을 그리면 될 것이다:
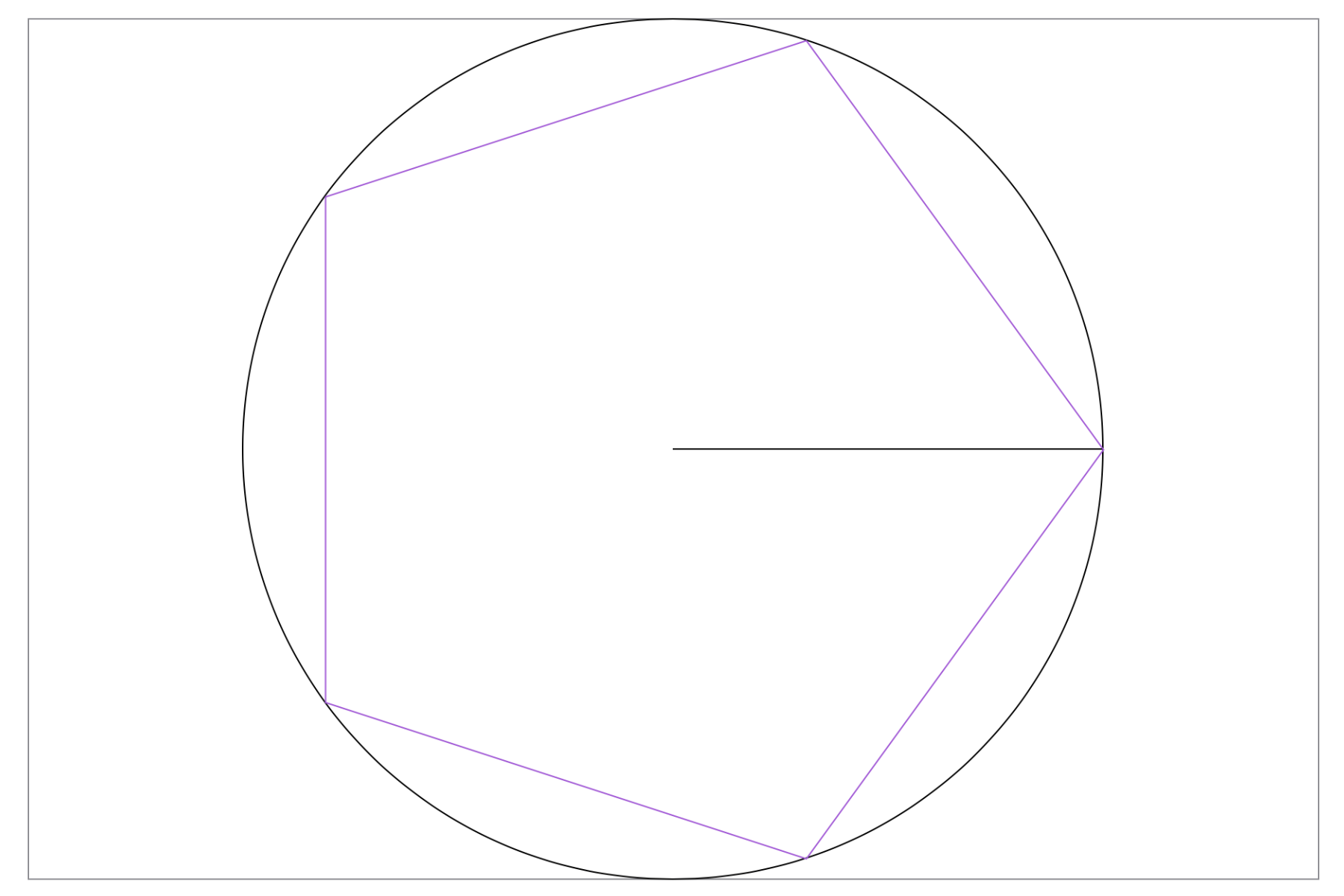
이를 위하여, 다음과 같이 CGRect에 간단한 computed property 둘을 추가하였다:
import CoreGraphics
extension CGRect {
var localCenter: CGPoint { CGPoint(x: width / 2, y: height / 2) }
var minSide: CGFloat { min(width, height) }
}localCenter는 CGRect의 중심점을 해당 CGRect의 좌표계에서 표시한 값이다.
즉, 그냥 width와 height 각각의 절반을 좌표로 가지는 CGPoint이다.
또한 minSide는 width와 height 중 작은 값이다.
그리고 원에서 등간격으로 벌어진 CGPoint들을 쉽게 찍을 수 있도록
CGPoint에도 유용한 method 둘을 추가하였다:
extension CGPoint {
func offset(x: CGFloat = 0, y: CGFloat = 0) -> CGPoint {
CGPoint(x: x + self.x, y: y + self.y)
}
func centeredConcyclic(radius: CGFloat, angle: CGFloat) -> CGPoint {
offset(x: radius * cos(angle), y: radius * sin(angle))
}
}offset(x:y:) 함수는 그냥 x와 y만큼 떨어진 새로운 점을 반환한다.
이때 유의할 점은, iOS 좌표계의 y축은 화면 위에서 아래로 향하는 방향이다.
일반적으로 우리가 생각하는 직교 좌표계를 축 대칭한 형태다.
이는 다음 함수인 centeredConcyclic(radius:angle:)을 사용할 때 유의해야하는
부분인데, angle은 반시계 방향이 아니라 시계 방향으로 도는 각도이다.
(수학의 극좌표에 익숙하지 않다면 오히려 다행인 것이, 일반적으로 수학에서는
반시계 방향을 기준으로 생각한다.)
극좌표계와 직교좌표계의 변환 공식에서 회전각을 시계 방향으로 생각하면 된다.
즉, 를 쓸 때 는 시계 방향으로
회전한 각도이다.
정리하자면, centeredConcyclic(radius:angle:)은 주어진 CGPoint를
중심으로 하는 반지름 radius의 원에서, 축으로부터 시계 방향으로 회전한
CGPoint이다.
이제 정다각형을 나타내는 struct RegularPolygon을 구현할 모든 준비가 되었다.
RegularPolygon은 변의 개수인 sides를 받아서 만들도록 구현한다:
struct RegularPolygon: Shape {
var sides: Int
func path(in rect: CGRect) -> Path {
let radius = rect.minSide / 2
let origin = rect.localCenter
var path = Path()
for i in 0..<sides {
let cyclicPoint = origin.centeredConcyclic(
radius: radius,
angle: 2 * .pi * CGFloat(i) / CGFloat(sides)
)
if i == 0 {
path.move(to: cyclicPoint)
} else {
path.addLine(to: cyclicPoint)
}
}
path.closeSubpath()
return path
}
}거의 자명한 코드인데, for 문 안에서는 축에서부터 시계 방향으로 sides개의
CGPoint들을 등간격으로 찍는다.
cyclicPoint는 한 바퀴에 해당하는 를 sides등분 한 것이므로 2 * .pi * CGFloat(i) / CGFloat(sides)만큼 회전한 것이다.
(이때 .pi는 CGFloat.pi인데, Double.pi도 있고 Float.pi도 있다.)
i가 0인 경우는 처음 시작할 때이므로 move(to:)로 선을 긋지 않고 이동만
하며, 이후로는 addLine(to:)로 선을 긋는다.
마지막 꼭짓점을 찍은 후 첫 번째 꼭짓점까지 다시 선분을 연결하기 위해
closeSubpath()를 호출하면 정다각형이 완성된다.
실은 위의 보라색 오각형이 SwiftUI에서 RegularPolygon을 사용해 그린 것이다.
Sierpinski 삼각형
Shape을 구현했으니 Sierpinski 삼각형은 금방이다.
특히 Sierpinski 삼각형은 자기 자신의 형태를 위에 하나, 아래에 양 옆으로 두 개만
포함하므로 간단하다.
바로 구현을 제시하자면 아래와 같다:
struct Triangle: View {
let step: Int
private var child: some View { Triangle(step: step - 1) }
private var bottomRow: some View {
HStack(spacing: 0) { child; child }
}
var body: some View {
if step > 0 {
return GeometryReader { geometry in
VStack(spacing: 0) {
self.child
.frame(width: geometry.size.width / 2)
self.bottomRow
.frame(width: geometry.size.width)
}
}
.aspectRatio(contentMode: .fit)
.asAnyView()
} else {
return RegularPolygon(sides: 3)
.rotationEffect(.radians(.pi / 6))
.aspectRatio(contentMode: .fit)
.asAnyView()
}
}
}child는 step을 하나 줄인 단계의 Triangle이고, bottomRow는 아랫줄에 올
child 두 개의 HStack이다.
여기서 Triangle의 비율을 유지하기 위해 GeometryReader을 사용해 명시적으로
윗줄의 child는 아랫줄의 bottomRow의 너비를 각각 전체 너비의 절반, 그리고
동일하게 설정해줬다.
또한 .aspectRatio(contentMode: .fit)으로 늘어나지 않고 작은 너비에 맞게 비율을
조절하였다.
이는 남은 공간을 모두 채우도록 view를 늘이는 ContentMode.fill와 함께
enum ContentMode의 두 case 중 하나다.
마지막으로 종료 조건은 else 문의 RegularPolygon(sides: 3)로 시작하는
View인데, rotationEffect(.radians(.pi / 6))은 RegularPolygon의 첫 꼭짓점이
(RegularPolygon의 중심을 원점으로 하는 local 좌표계의) 축 상에 존재하기
때문에 회전시켜준 것이다.
이의 유용한 부작용으로는, RegularPolygon의 크기에 비례하는 margin이 생긴다는
점이다.
이것은 위에서 Sierpinski 카펫을 다시 RegularPolygon(sides: 4)로 구현한
이유기도 하다.
또한
GitHub의 버전에서는
각 RegularPolygon(sides: 3)가 회전할 수 있게 angle을 주었는데, 처음
RegularPolygon을 설계할 때 주어진 CGRect의 내접원에 내접하는 정다각형으로
하였기 때문에 회전하여도 서로 겹치지 않게 된다.
서로 겹치지 않는다는 것은 아래 GIF를 통해 확인할 수 있다:

구현한 Sierpinski 삼각형은 step = 0부터 9에 대해서 아래와 같다:










(GitHub에서 프로젝트를 바로 받아 Xcode로 실행해보면 step = 9까지는 성능 상의
이유로 늘리지 못하게 해놓았지만, 확인하고 싶다면 ContentView의 maxStep을
수정하면 된다.)
Fractal Tree와 애니메이션
마지막으로, fractal tree의 구현을 알아보자.
이를 위해서는 위의 Sierpinski 카펫이나 삼각형과는 접근을 좀 다르게 해야하는데,
선분 등은 Shape 자체에서 구현을 해야 하기 때문이다.
(아마도, 시도해보지는 않았지만) path(in:) 자체를 재귀함수로 구현할 수
있겠지만, 위에서 보았듯이 성능 상의 이유로 fractal tree의 구현은 직접
반복문으로 구현하였다.
사실, 위의 두 Sierpinski 도형도 (마찬가지로 시도하지 않았지만) path(in:)
자체에서 반복문으로 구현할 수 있을 것이다.
다만 애초의 선언적인 방식으로 구성하고 싶었던 목적과는 맞지 않을 뿐이다.
Queue
Fractal tree의 각 꼭짓점에 도달하면, 다시 해당 꼭짓점에서 fractal tree를 그려 나가야 한다. 그리고 우리는 모든 가지의 깊이를 동일하게 맞추고 싶기 때문에, 너비 우선 탐색으로 각 꼭짓점에 방문하여 fractal tree를 구현하면 좋을 것 같다. 너비 우선 탐색(breadth-first search, 이하 BFS)이란, 자식 꼭짓점에 방문하기 전에 같은 계층의 부모 꼭짓점들을 모두 다 방문하는 것이다. 이 방식으로는 깊이 의 꼭짓점들은 모두 깊이 꼭짓점들보다 먼저 방문하게 된다. 예컨대 fractal tree에서는 다음과 같은 순서로 방문하는 것이다:
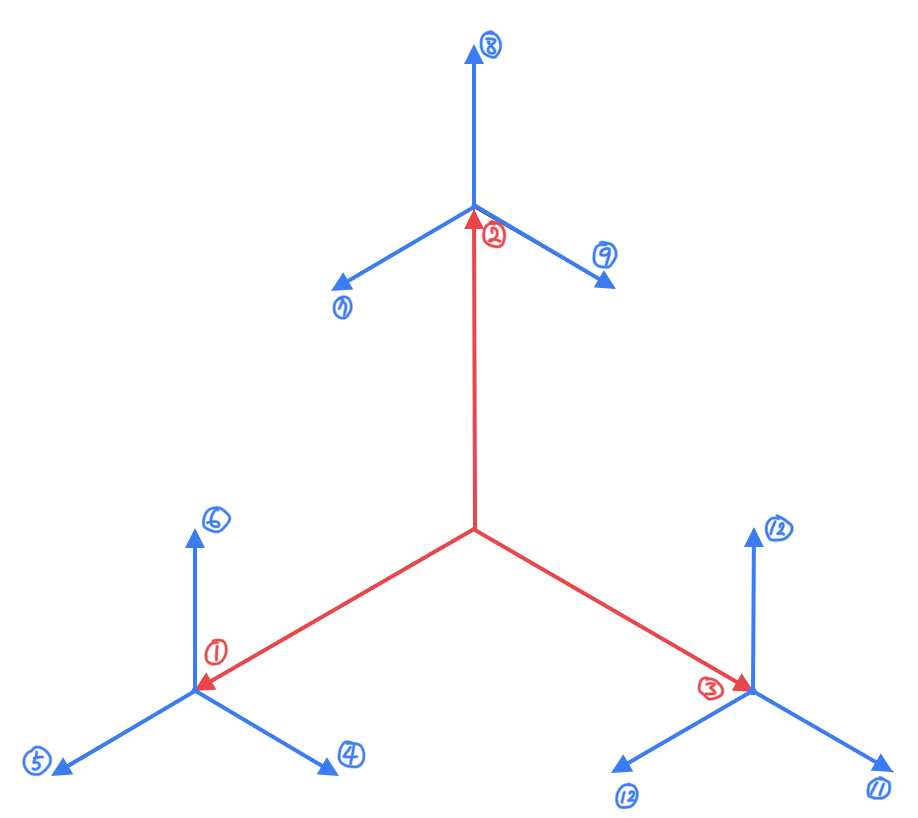
사실 우리는 각 꼭짓점에 정확히 세 개의 변들이 연결된 것을 알고 있고, 정확히는 탐색을 하는 것이 아니라 생성을 하는 것이므로 완전한 BFS 알고리즘을 구현할 필요가 없다.
일단 BFS를 위해서 queue를 구현해야 한다. Swift에는 안타깝게도 일반적인 queue 자료 구조가 없기 때문에 직접 구현해야 한다. 여기서는 queue에 들어갈 원소의 적당한 상한 값을 이미 알 수 있으므로 (생성하고 싶은 깊이를 미리 정하므로), 그리고 병목은 자료의 수가 아니라 SwiftUI 그 자체이므로, 연결 리스트가 아니라 배열 기반의 구현을 하였다.
개략적으로 설명하자면, 먼저 담을 수 있는 최대 크기를 정한 후 해당 크기의
Array를 초기화한다.
원소를 queue에 추가(enqueue)할 때마다 tail index를 하나씩 증가시키고, 반대로
원소를 제거(dequeue)할 때마다 head index를 하나씩 증가시켜 queue의 처음
위치와 마지막 위치를 표시한다.
Index를 증가시키는데 배열의 끝에 도달하면, 다시 index 0으로 '감싼다'.
이때 tail은 마지막 원소의 다음 자리를 표시하며, queue가 비어있을 때는
head와 tail이 같을 때이다.
따라서 이 queue 구현은 Array의 크기보다 하나 작은 수의 원소를 담을 수 있다.
실제 Swift 구현은 아래와 같다:
struct Queue<Element> {
/// A queue can store at most `capacity - 1` elements
let capacity: Int
private var container: [Element?]
private var head: Int
private var tail: Int
var isEmpty: Bool { head == tail }
mutating func enqueue(_ newElement: Element) -> Bool {
if head == 0 && tail == capacity - 1 || head == tail + 1 {
// The queue is full
return false
}
container[tail] = newElement
tail = tail == capacity - 1 ? 0 : tail + 1
return true
}
mutating func dequeue() -> Element? {
if head == tail {
// The queue is empty
return nil
}
guard let result = container[head] else {
assertionFailure("container should not be empty as head != tail")
return nil
}
head = head == capacity - 1 ? 0 : head + 1
return result
}
init(_ array: [Element] = [], capacity: Int) {
precondition(
capacity > array.count,
"capacity must be greater than the number of elements in the array"
)
self.capacity = capacity
container = [Element?](repeating: nil, count: capacity)
for (i, e) in array.enumerated() {
container[i] = e
}
head = 0
tail = array.count
}
}Queue는 Element에 대한 generic으로 구현을 하였고, 내부적으로 가지고 있는
배열 container은 Element?의 Array로, 처음 입력된 값을 빼고는 nil로
초기화되어 있다.
함수 구현은 위에 설명한 것과 거의 같은데, enqueue(_:)와 dequeue() 함수에서는
각각 overflow와 underflow의 경우 예외 처리를 해주었다.
enqueue(_:)의 경우 반환값이 false인 경우 queue가 가득 차서 새로운
Element를 넣지 못한 것이고, dequeue()의 경우 반환값이 nil이면 queue에
원소가 없는 경우이다.
또한 dequeue를 한다고 실제 값을 지우는 것은 아니고 head index만 조절할
뿐이다.
초기화는 편의를 위해 바로 array: [Element]로부터 만들 수 있게 하였다.
전체적으로 굉장히 단순한 구현이지만, 우리의 목적에는 충분히 부합한다.
Fractal tree 구현을 하기 전에 마지막으로, 유향 선분을 나타내는
struct DirectedLineSegment를 구현한다.
DirectedLineSegment
CoreGraphics에 CGVector이 있기는 한데, 이는 크기와 방향만을 가지기 때문에
시작점과 끝점이 필요한 우리의 요구와는 맞지 않다.
따라서 직접 유향 선분을 나타내는 DirectedLineSegment을 구현하였다.
이는 fractal tree를 만들 때 특정 선분의 방향으로 연장하고 회전하는 것을
반복해야 하기 때문에 유용하다.
가지고 있는 변수는 시작점 start와 끝점 end으로 단 두 개이다:
import CoreGraphics
struct DirectedLineSegment {
var start: CGPoint
var end: CGPoint
var dx: CGFloat { end.x - start.x }
var dy: CGFloat { end.y - start.y }
var magnitude: CGFloat { sqrt(dx * dx + dy * dy) }
var direction: CGFloat { atan2(dy, dx) }
/// Returns a point extended in the direction rotated clockwise by `angle`
/// with a distance `multiple` times the magnitude of this line segment.
func extended(multiple: CGFloat, angle: CGFloat) -> CGPoint {
end.centeredConcyclic(
radius: multiple * magnitude,
angle: direction + angle
)
}
}dx, dy, magnitude, direction은 각각 변위, 변위, 길이, 그리고
방향이다.
direction은 위에서 강조하였듯이 시계 방향으로의 각도로,
atan2로 쉽게 구할 수 있다.
(필자도 처음 시도할 때는 그냥 atan과 switch로 구현하려고 했는데, 좌표축도
뒤집혀 있고 CGFloat 연산의 부정확함에 따른 굉장히 작은 음수/양수 오차의
등장으로 삽질을 하다가 atan2를 기억하였다.)
extended(multiple:angle:) 함수는 유향 선분의 끝점에서부터 angle만큼 시계
방향으로 회전한 후, 유향 선분의 길이의 multiple 배만큼 나아간 위치의
CGPoint를 반환한다.
구현은 위에서 만든 centeredConcyclic(radius:angle:)로 간단히 할 수 있다.
Fractal Tree
Fractal tree는 반시계 방향, 일직선, 그리고 시계 방향 세 방향으로 선분 긋기를
반복하면 된다.
이때 선분의 길이는 매번 절반씩 짧아지게 된다.
이때 처음 시작점은 주어진 CGRect의 중심에서 아래로 높이의 만큼
떨어진 곳으로, 첫 선분들의 길이는 CGRect의 변 중 짧은 것의 로
하였다.
정삼각형 기준으로 생각한다면 변의 길이가 딱 맞는 것보다 짧은 것인데, 이는
fractal tree의 각 선분들이 떨어져 있는 각을 보다 작은 경우, 특히
인 경우 CGRect 밖으로 나가지 않게 하기 위함이다.
그렇다면 현재까지의 코드는 다음과 같다:
struct Tree: Shape {
var step: Int
var angle: CGFloat = .pi * 2 / 3
func path(in rect: CGRect) -> Path {
guard step > 0 else { return Path() }
let origin = rect.localCenter.offset(y: rect.height / 6)
let radius = rect.minSide / 4
let turnAngles = [-angle, 0, angle]
var path = Path()
return path
}
}이때 step과 angle은 각각 진행할 깊이, 각 선분이 분리된 (라디안) 각이다.
이제 origin에서 radius 길이의 선분을 turnAngles의 각 원소만큼 시계
방향으로 회전하여 그으면 깊이 1에 대한 fractal tree가 된다.
이는 .centeredConcyclic(radius:angle:)을 사용하여 쉽게 할 수 있다.
다만, 여기서 angle 값은 위에서 설명하였듯이 원의 중심에서 축 방향이 0인
기준이기 때문에 fractal tree의 가운데 선분이 위로 향하기 위해서는
turnAngles의 값에 각각 시계 방향으로 회전하여 CGFloat.pi / 2를
빼서 .centeredConcyclic(radius:angle:)의 angle 인자로 넣어야 한다.
이렇게 만든 선분은 위에서 구현한 DirectedLineSegment으로 표현할 것이다:
let initialSegments: [DirectedLineSegment] = turnAngles.map {
// (- pi / 2), as the +y direction is downwards
let angle = $0 - CGFloat.pi / 2
let end = origin
.centeredConcyclic(radius: radius, angle: angle)
return DirectedLineSegment(start: origin, end: end)
}첫 세 선분들 initialSegments를 먼저 화면에 그려보고 싶다면,
func path(in rect: CGRect) -> Path {
guard step > 0 else { return Path() }
let origin = rect.localCenter.offset(y: rect.height / 6)
let radius = rect.minSide / 4
let turnAngles = [-angle, 0, angle]
let initialSegments: [DirectedLineSegment] = turnAngles.map {
// (- pi / 2), as the +y direction is downwards
let angle = $0 - CGFloat.pi / 2
let end = origin
.centeredConcyclic(radius: radius, angle: angle)
return DirectedLineSegment(start: origin, end: end)
}
var path = Path()
for segment in initialSegments {
path.move(to: segment.start)
path.addLine(to: segment.end)
}
return path
}와 같이 initialSegments의 각 segment별로 path를 그려주면 된다.
결과는 다음과 같다:
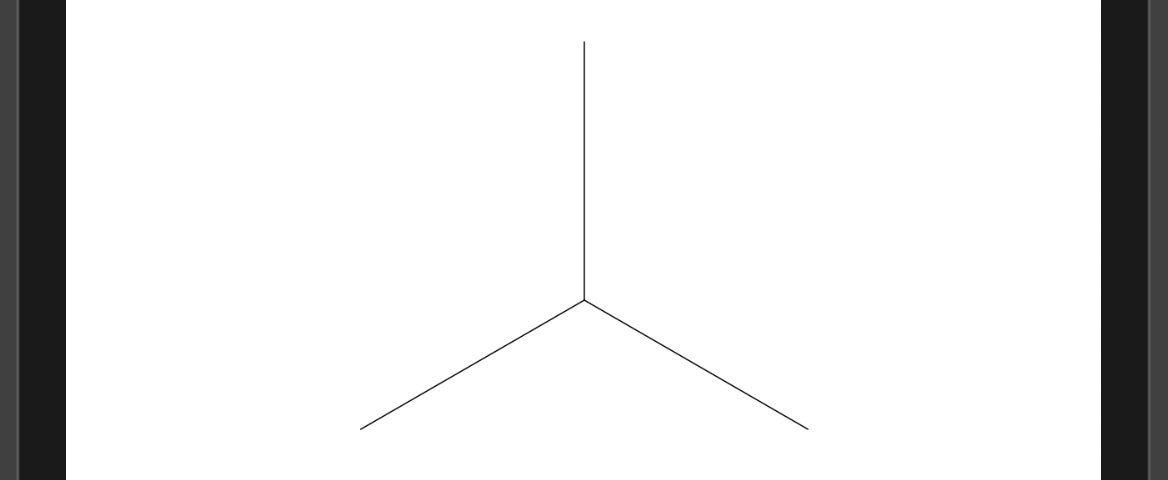
이때 preview를 위해서는 .stroke(lineWidth: 0.5)와
.aspectRatio(contentMode: .fit)을 적용해주었다.
이제 주어진 임의의 step 깊이의 fractal tree를 그려야 한다.
step에 대해서 그려야하는 선분의 길이는 이다.
정수의 지수를 빠르게 계산하기 위해서 필자는 다음과 같은 Int extension을
만들었다:
extension Int {
static func pow(_ base: Int, _ exponent: Int) -> Int {
var base = base
var exponent = exponent
var result = 1
while true {
if !exponent.isMultiple(of: 2) {
result *= base
}
exponent /= 2
if exponent == 0 { break }
base *= base
}
return result
}
}지수 exponent를 절반씩 분할하여 계산하는 방법으로, 로그 시간 시간 복잡도를
가진다.
어차피 너무 큰 step에 대해서는 그림을 그리는 것이 병목이기도 하고, 따라서
미리 3의 거듭 제곱들을 dictionary로 저장해도 되지만 필자는 일반성을 위해
위와 같이 runtime에 계산하기로 하였다.
이제 initialSegments를 구현한 Queue에 넣고, 각 segment를 꺼낸 후 새로운 세
개의 segment들을 넣는 것을 회 반복하면 된다.
미리 Queue의 크기를 정해줘야 하는데, 아무리 커도 보다는 작으므로 이를 넉넉한
상한으로 잡자.
이 과정은 다음과 같다:
let power = Int.pow(3, Int(step))
var queue = Queue(initialSegments, capacity: 4 * power)
var path = Path()
for _ in 0..<3 * (power - 1) / 2 {
let segment = queue.dequeue()!
path.move(to: segment.start)
path.addLine(to: segment.end)
let nextPoints = turnAngles
.map { segment.extended(multiple: 0.5, angle: $0) }
for point in nextPoints {
guard queue.enqueue(
DirectedLineSegment(start: segment.end, end: point)
) else {
assertionFailure("Queue overflow")
return path
}
}
}nextPoints는 각 선분의 끝에서 나아갈 새로운 세 선분의 꼭짓점들이다.
처음에 dequeue는 계산한 것이 맞다면 반드시 dequeue할 수 있음이 보장되며,
enqueue의 경우는 queue의 크기가 충분하다면 성공할 것이다.
(위에서 enqueue가 성공 여부를 Bool로 반환하도록 구현하였다.)
지금까지의 코드를 하나로 합치면 다음과 같다:
struct Tree: Shape {
var step: Int
var angle: CGFloat = .pi * 2 / 3
func path(in rect: CGRect) -> Path {
guard step > 0 else { return Path() }
let origin = rect.localCenter.offset(y: rect.height / 6)
let radius = rect.minSide / 4
let turnAngles = [-angle, 0, angle]
let initialSegments: [DirectedLineSegment] = turnAngles.map {
// (- pi / 2), as the +y direction is downwards
let angle = $0 - CGFloat.pi / 2
let end = origin
.centeredConcyclic(radius: radius, angle: angle)
return DirectedLineSegment(start: origin, end: end)
}
let power = Int.pow(3, Int(step))
var queue = Queue(initialSegments, capacity: 4 * power)
var path = Path()
for _ in 0..<3 * (power - 1) / 2 {
let segment = queue.dequeue()!
path.move(to: segment.start)
path.addLine(to: segment.end)
let nextPoints = turnAngles
.map { segment.extended(multiple: 0.5, angle: $0) }
for point in nextPoints {
guard queue.enqueue(
DirectedLineSegment(start: segment.end, end: point)
) else {
assertionFailure("Queue overflow")
return path
}
}
}
return path
}
}이렇게 작성한 결과, Tree(step: 7, angle: .pi * 2 / 3)를 그리면 다음과 같다:
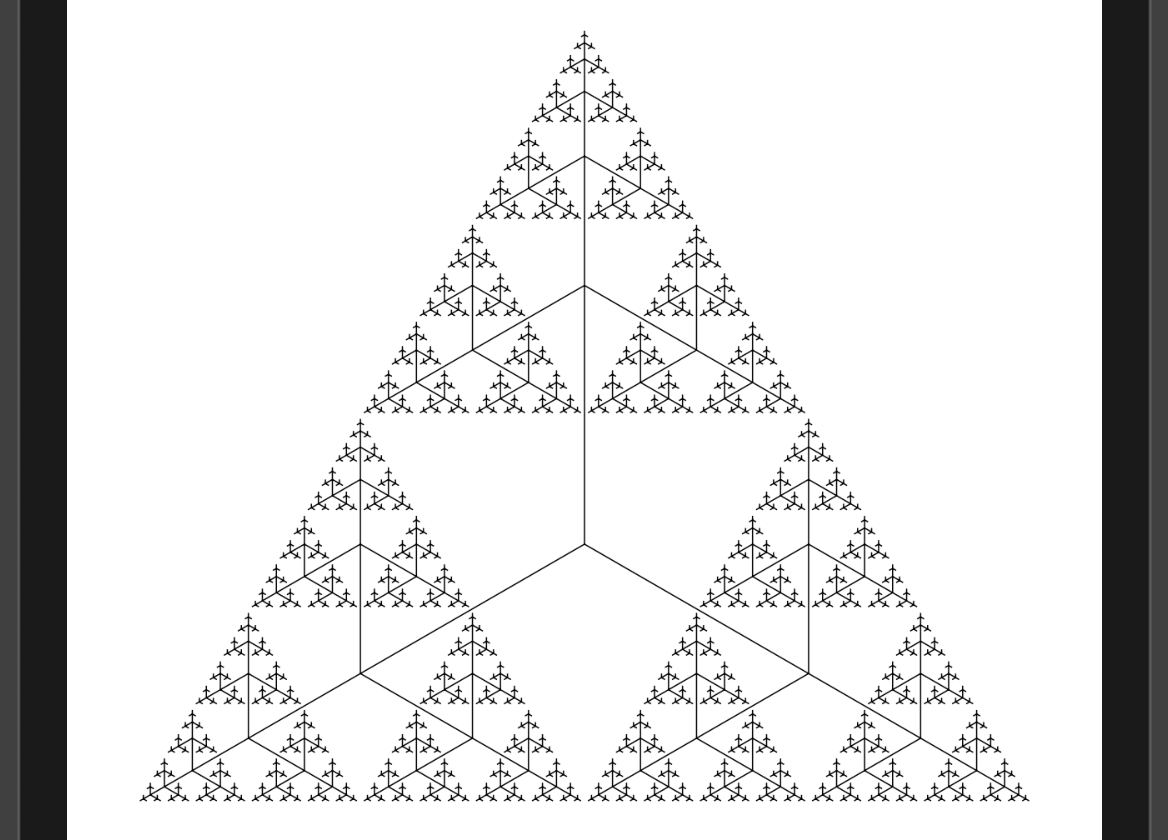
마찬가지로 preview를 위해 .stroke(lineWidth: 0.5)와
.aspectRatio(contentMode: .fit)을 적용해주었다.
Demonstration View
필자는 직접 step이랑 angle을 조절할 수 있는 UI를 만들었다.
이는 Tree에 직접 구현하지 않고, 위의 Carpet과 Triangle까지 포함할 수
있도록 wrapper의 형태로 구성하였다:
struct Demonstration<F>: View where F: Fractal {
let maxStep: Int
let maxAngle: Double
@State private var step = 2
@State private var angle = 0.0
var body: some View {
VStack {
F(step: step, angle: angle)
.drawingGroup()
Stepper("Step \(step)", value: $step, in: 0...maxStep)
.fixedSize()
Slider(value: $angle, in: 0...maxAngle)
.padding([.horizontal, .bottom])
}
.navigationBarTitle("\(F.name)")
}
init(maxStep: Int, maxAngle: Double) {
self.maxStep = maxStep
self.maxAngle = maxAngle
}
}이때 Fractal protocol은 다음과 같이 정의되었다:
protocol Fractal: View {
static var name: String { get }
init(step: Int, angle: Double)
}Fractal는 Carpet, Triangle, 그리고 Tree가 따르도록 할 것이다.
먼저 Demonstration<F>를 보자면, 주어진 F와 Stepper, Slider가 VStack을
이루는 간단한 구조이다.
Stepper는 step을, Slider는 angle을 조절하는 control이다.
Tree는 Fractal에 따르도록 wrapper를 만들었다.
위에 구현한 Tree는 TreeShape로 변경하고, 아래와 같이 새로운 Tree
wrapper를 만들었다:
struct Tree: Fractal {
static var name: String { "Fractal Tree" }
var step: Int
var angle: Double = .pi * 2 / 3
var body: some View {
TreeShape(step: step, angle: angle)
.stroke(lineWidth: 0.5)
.aspectRatio(contentMode: .fit)
}
struct TreeShape: Shape {
// 원래의 Tree를 여기로 옮겼다
}
}이를 Demonstration에 감싸
Demonstration<Tree>(maxStep: 10, 8, maxAngle: .pi * 2 / 3)와 같이 하면,
다음과 같이 control로 fractal tree를 조절할 수 있다:
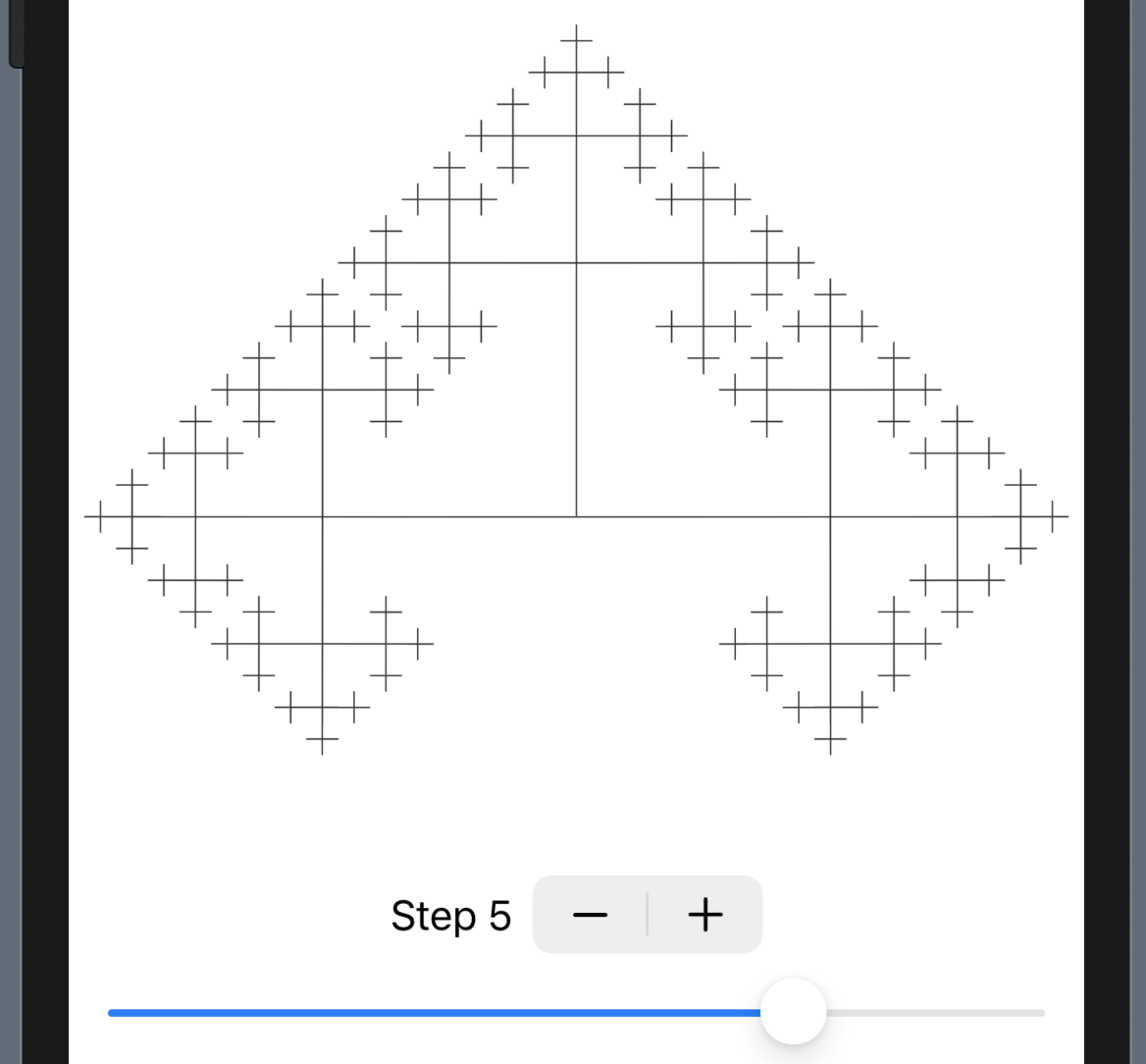
애니메이션
위의 Demonstration<Tree>에서 한 가지 아쉬운 점이 있는데, step을 증가시킬 때
fractal tree이 바로 바뀐다는 점이다.
우리의 fractal tree는 엄연히 나무인데 자라는 모습을 볼 수 없다니!
step을 증가시키거나 감소시키면 부드럽게 fractal tree의 가지가 자라고 줄어드는
것을 볼 수 있도록 애니메이션을 구현해 보았다.
SwiftUI에서 애니메이션은 Animatable protocol을 따르면 된다.
이는 애니메이션이 가능한 var animatableData를 구현하면 되는데, Shape는
Animatable을 이미 따르고 있다.
animatableData는 VectorArithmetic을 따르는 type에 해당하면 되는데,
Double, Float, CGFloat는 이미 여기에 해당한다.
우리는 step을 animatableData로 하고 싶지만, 바로 적용할 수는 없다.
step은 Int이기 때문이다.
그렇다고 step을 무작정 Double로 바꾼다고 되는 것도 아니다.
SwiftUI가 step = 2.136와 같은 값을 그릴 수 있도록 알려줘야 하기 때문이다.
step에 따라 마지막 leaf node들에 대하여 길이를 연속적으로 증가시키면 될
것이다.
먼저 step으로 바로 Double로 만들지 말고, step은 Int로 그대로 두고
Double인 _step을 만든 후 이를 animatableData로 해준다:
struct TreeShape: Shape {
var step: Int
private var _step: Double
var angle: CGFloat = .pi * 2 / 3
var animatableData: Double {
get { _step }
set { _step = newValue }
}
func path(in rect: CGRect) -> Path {
// ...
}
}Leaf node인 경우 path(in:)의 while 문의 path.addLine(to: segment.end)
부분을 다르게 처리해주면 된다.
기존과 달라진 부분을 적어보면:
// ...
let roundedStep = _step.rounded(.up)
let power = Int.pow(3, Int(roundedStep))
var queue = Queue(initialSegments, capacity: 4 * power)
var path = Path()
for i in 0..<3 * (power - 1) / 2 {
let isLeafNode = i >= (power - 3) / 2
let segment = queue.dequeue()!
path.move(to: segment.start)
if isLeafNode {
path.addLine(
to: segment.extended(
multiple: CGFloat(roundedStep - _step),
angle: -.pi
)
)
} else {
path.addLine(to: segment.end)
}
// ...여기서 roundedStep는 _step을 올림한 값이며, isLeafNode는 현재 반복문의
index i가 마지막 leaf node에 대한 것인지 확인하는 flag이다.
만약 isLeafNode라면, path에서 연장할 길이가 원래보다 짧아야 할 것이다.
이는 extended를 사용하여, 반대 방향 (angle: -.pi)으로 0과 1 사이의 값인
roundedStep - _step 배 이동한 점까지만 선을 긋도록 수정하였다.
이렇게 구현한 Tree의 전체 코드는 다음과 같다:
struct Tree: Fractal {
static var name: String { "Fractal Tree" }
var step: Int
var angle: Double = .pi * 2 / 3
var body: some View {
TreeShape(step: step, angle: angle)
.stroke(lineWidth: 0.5)
.animation(step <= 6 ? .default : .none)
.aspectRatio(contentMode: .fit)
}
}
extension Tree {
struct TreeShape: Shape {
var step: Int
private var _step: Double
// var sides: Int = 3
var angle: CGFloat = .pi * 2 / 3
var animatableData: Double {
get { _step }
set { _step = newValue }
}
func path(in rect: CGRect) -> Path {
guard step > 0 else { return Path() }
let origin = rect.localCenter.offset(y: rect.height / 6)
let radius = rect.minSide / 4
let turnAngles = [-angle, 0, angle]
let initialSegments: [DirectedLineSegment] = turnAngles.map {
// (- pi / 2), as the +y direction is downwards
let angle = $0 - CGFloat.pi / 2
let end = origin
.centeredConcyclic(radius: radius, angle: angle)
return DirectedLineSegment(start: origin, end: end)
}
// Lower bound for the queue size
// < 3^step + 3^(step + 1) = 4 * 3^step
// Total number of dequeue count =
// 3 + 3^2 + ... + 3^step = 3 * (3^step - 1) / 2
let roundedStep = _step.rounded(.up)
let power = Int.pow(3, Int(roundedStep))
var queue = Queue(initialSegments, capacity: 4 * power)
var path = Path()
for i in 0..<3 * (power - 1) / 2 {
let isLeafNode = i >= (power - 3) / 2
let segment = queue.dequeue()!
path.move(to: segment.start)
if isLeafNode {
path.addLine(
to: segment.extended(
multiple: CGFloat(roundedStep - _step),
angle: -.pi
)
)
} else {
path.addLine(to: segment.end)
}
let nextPoints = turnAngles
.map { segment.extended(multiple: 0.5, angle: $0) }
for point in nextPoints {
guard queue.enqueue(
DirectedLineSegment(start: segment.end, end: point)
) else {
assertionFailure("Queue overflow")
return path
}
}
}
return path
}
init(step: Int, angle: Double) {
self.step = step
self._step = Double(step)
self.angle = CGFloat(angle)
}
}
}Finale
제목이 '프랙탈과 애니메이션'이지만, 글을 작성하다보니 애니메이션의 부분이 짧게 마무리가 되었다. 하지만 그만큼 SwiftUI에서 애니메이션을 쉽게 넣을 수 있다는 것을 알 수 있다.
GitHub에는 위의 구현 이외에도,
Combine과 Timer, 그리고 EnvironmentObject를 사용해 자동으로
F: Fractal의 매개변수를 조절하는 코드가 Demonstration에 들어가 있다.
나아가, step이 큰 경우에는 iOS 기기의 한계로 인해 애니메이션이 실행될 경우
느리거나 앱이 종료하는 문제가 있기 때문에, 애니메이션을 진행할 최대 step을
제한하고 Toggle을 비활성화시키는 코드 등이 들어 있다.
또한 위에서 언급하였듯이 Sierpinski 카펫의 경우 RegularPolygon으로 다시
구현이 되었으며, Sierpinski 삼각형과 마찬가지로 각 도형이 회전하도록
Fractal의 angle을 활용하게 구현이 되어 있다.
지금까지 SwiftUI에서 fractal을 구현하는 선언적인 방식과 Shape를 사용한 두
가지 방법과, Animatable을 사용한 애니메이션에 대해 알아보았다.